포스팅 목차
Time Domain과 Frequency Domain 은 학부 과정 중에서도 자주 들어본 내용이지만, 이론과 원리를 배운 상황이며 필요성과 사용하는 곳에 대해서는 되게 무지했었던 것 같다.
이러한 내용들을 토대로 대체로 이해하기 쉽게 따로 정리해보았다.
1. Time Domain
한국어로 간단하게 풀이하자면 시간의 관점에서 해석이다.
X축을 시간, Y축을 신호로 시간에 따른 신호 크기의 변화를 직관적으로 확인할 수 있다.
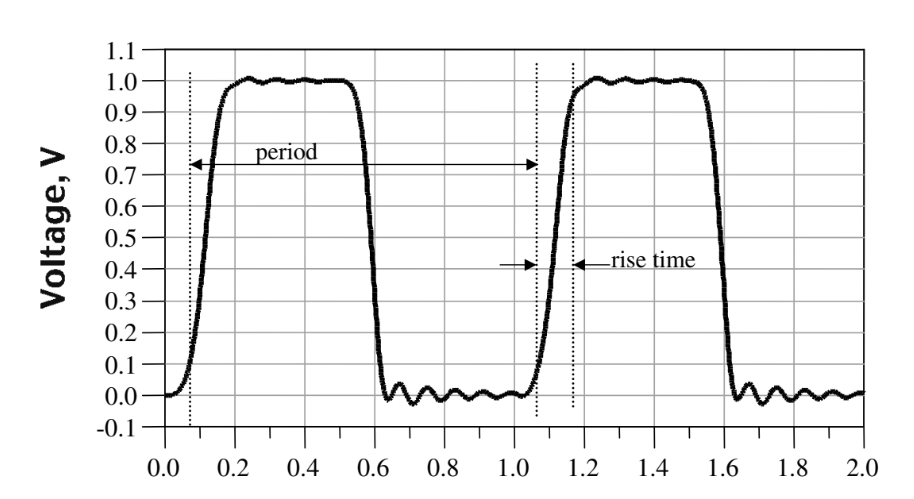
예시로 아래 그림의 Clock Wave form을 보면서 우리는 Clock의 주기, Rise time 등의 다양한 정보를 할 수 있고,
2차적으로는 Clock의 Frequecy 등도 계산해볼 수 있다.
2. Frequency Domain
주파수 관점에서의 해석은 수학적인 접근이다. 이로 인해서 Frequency Domain을 통한 해석은 관련 분야에 대한 이해가 필요하다.
주파수 관점에서 가장 중요한 법칙은 모든 주파수는 Sine Wave를 통해서 나타낼 수 있다는 점이다. Sine 함수는 아래 4가지 중요 특성을 가지고 있고, 이를 통해서 주파수를 표현하고 해석할 수 있다. 아래와 같은 성질을 토대로 Sine 함수를 통한 Frequency 해석을 용이하게 할 수 있다.
- Time Domain 의 함수를 완벽하고 오직 단일한 함수로 묘사할 수 있다.
- 다른 주파수를 가지고 있는 Sine wave는 직교한다. (직교 함수, 함수를 곱해서 내적 할 경우 0이 나오는 상황; 두 함수를 분리할 수 있다는 것에 장점이 있다.)
- 수학적으로 잘 정리되어짐
- 모든 부분에서 값이 존재하며, 미분 값 또한 그렇다.
사실, Frequency Domain의 구성 정보는 Time Domain과 같다. Signal/Power를 분석하는 것에 유용하여 사용하는 것이니 참고하면 좋을 것 같다. (ex. Bandwidth, impedance)
3. The Fourier Transform
주구장창 좋다고 이야기한 Frequency Domain을 사용하기 위해서는 필수적인 것이
Fourier Transform이다. 이 방법을 통해서 Time domain의 함수를 Frequency Domin으로 변환이 가능하다.
The Fourier Transform 은 아래 3 가지 종류가 있다. (자세한 내용은 너무 어려워서 포기)
- Fourier integral (Time -> Frequency 로의 수학적이고 이상적인 변환)
- Discrete Fourier Transform (DFT) (주기성, 반복성의 가정으로 간단한 수학적인 기술로 변환 가능)
- Fast Fourier Transform(FFT) (DFT와 유사, matrix algebra를 사용한 간단한 계산으로 변환 가능)
내 생각
Sine 함수를 Frequency Domain에 적용하는 것은, 실제로는 Sine 함수를 Tool로 사용하는 느낌이 강하다. 표현과 수학적 풀이, 해석에 용이하기에 사용하는 것이지, '모든 Wave를 Sine 함수이다'라는 기초로 시작한 것은 아닌 것으로 생각된다.
'SIPI' 카테고리의 다른 글
| SI/PI 인접 컨덕터의 누화(Cross talk) 및 원하지 않는 신호 결합 (0) | 2023.07.16 |
|---|---|
| Time Domain and Frequency Domain (0) | 2023.06.29 |
| [SI/PI] Electrical Product Trend (0) | 2022.09.21 |
| [SI/PI] Signal Integrity 란 무엇인가? (EMI) (0) | 2022.09.04 |
| [SI/PI] Signal integrity 란 무엇인가(Cross talk, Rail collapse noise) (0) | 2022.08.26 |
